- rectangles
- squares
- rhombus
- trapezoids
Unlike my earlier post about quadrilaterals (see Coordinate Graphs of Quadrilaterals, dated July 2010), these problems focus on the properties of the diagonals and median of quadrilaterals.
These properties are as follows:- A diagonal divides a parallelogram into two congruent triangles (see Problems 1, 4 and 7).
- Diagonals of a parallelogram bisect each other, that is, the point of intersection of the diagonals is their midpoint (see Problems 1, 4 and 7).
- Midpoints of the sides of a parallelogram, when joined together, form another parallelogram (see Problems 2 and 3).
- Diagonals of a rhombus bisect its angles and are perpendicular to each other (see Problem 7).
- Diagonals of a rectangle are equal (see Problem 1 and 4).
- Diagonals of an isosceles trapezoid are equal (see Problem 5 and 6).
- The point of intersection of the diagonals of an isosceles trapezoid trisects the diagonals (see Problem 5 and 6).
- The median of a trapezoid is parallel to its bases (see Problem 6).
- The median of a trapezoid is equal to one half the sum of its bases (see Problem 6).
- The median of a trapezoid intersects each of its diagonals at their midpoints (see Problem 6).
Concepts Illustrated By the Problems
- distance between two points
- properties of parallel and perpendicular lines
- point of intersection of two straight lines
- equation of a straight line
- midpoint of a line segment
- angle between two lines
- angle bisector
Description of the Problems
Depending on the graph, a combination of the following information are provided:
- equations of the line segments
- slopes of the line segments
- x-intercepts and y-intercepts of the lines
- distances between the terminal points of the line segments
- midpoints of the line segments
Using one or a combination of two or more of the above information, it is possible for a problem to be presented in several ways.
Line segments and their terminal points referred to in the problems are the sides and vertices, respectively, of the quadrilaterals.
Slope of a line segment with terminal points A and B is abbreviated as mAB.
Distance between points A and B is abbreviated as distanceAB
Problem 1
.jpg)
Point of Intersection of the Diagonals: E (- 1/2, -1)
Distances Between Points
- distanceAB = distanceCD = √ 68
- distanceAD = distanceBC = √ 17
- distanceAC = distanceBD = √ 85
- distanceAE = distanceCE = distanceBE = distanceDE = √ 85/4
Equations of the Line Segments
- line segment AB : x - 4y + 5 = 0 (x-intercept = -5; y-intercept = 5/4)
- line segment BC : 4x + y - 14 = 0 (x-intercept = 14/4; y-intercept = 14)
- line segment CD : x - 4y - 12 = 0 (x-intercept = 12; y-intercept = -3)
- line segment AD : 4x + y + 20 = 0 (x-intercept = -5; y-intercept = -20)
- line segment AC : 2x + 9y + 10 = 0 (x-intercept = -5; y-intercept = -10/9)
- line segment BD : 6x - 7y - 4 = 0 (x-intercept = 2/3; y-intercept = - 4/7)
Slopes of the Line Segments
- mAB = mCD = 1/4
- mAD = mBC = -4
- mAC = - 2/9
- mBD = 6/7
Problem 2
.jpg)
Midpoints of Rectangle ABCD
- E (-1, 9/2)
- F (0, 0)
- G (-3,- 7/2)
- H (-4, 1)
Distances Between Points
- distanceAB = distanceCD = √ 17
- distanceAD = distanceBC = √ 68
- distanceEF = distanceFG = distanceGH = distanceEH = √ 85/4
- distanceAE = distanceBE = distanceCG = distanceDG = √ 17/4
- distanceAH = distanceDH = distanceBF = distanceCF = √ 17
Equations of the Line Segments
- line segment AB : x + 4y - 17 = 0 (x-intercept = 17; y-intercept = 17/4)
- line segment BC : 4x - y = 0 (x-intercept = 0; y-intercept = 0)
- line segment CD : x + 4y + 17 = 0 (x-intercept = -17; y-intercept = - 17/4)
- line segment AD : 4x - y + 17 = 0 (x-intercept = - 17/4; y-intercept = 17)
- line segment EF : 9x + 2y = 0 (x-intercept = 0; y-intercept = 0)
- line segment FG : 7x - 6y = 0 (x-intercept = 0; y-intercept = 0)
- line segment GH : 9x + 2y + 34 = 0 (x-intercept = -34/9; y-intercept = -17)
- line segment EH : 7x - 6y + 34 = 0 (x-intercept = -34/7; y-intercept = 17/3)
Slopes of the Line Segments
- mAB = mCD = - 1/4
- mAD = mBC = 4
- mEF = mGH = - 9/2
- mEH = mFG = 7/6
Problem 3
.jpg)
Midpoints of Square ABCD
- E (-1, 4)
- F (4, 1)
- G (1, -4)
- H (-4, -1)
Distances Between Points
- distanceAB = distanceBC = distanceCD = distanceAD = √ 68
- distanceEF = distanceFG = distanceGH = distanceEH = √ 34
- distanceAE = distanceBE = distanceBF = distanceCF = distanceCG = distanceDG = distanceAH = distanceDH = √ 17
Equations of the Line Segments
- line segment AB : x - 4y + 17 = 0 (x-intercept = -17; y-intercept = 17/4)
- line segment BC : 4x + y - 17 = 0 (x-intercept = 17/4; y-intercept = 17)
- line segment CD : x - 4y - 17 = 0 (x-intercept = 17; y-intercept = - 17/4)
- line segment AD : 4x + y + 17 = 0 (x-intercept = - 17/4; y-intercept = -17)
- line segment EF : 3x + 5y - 17 = 0 (x-intercept = 17/3; y-intercept = 17/5)
- line segment FG : 5x - 3y - 17 = 0 (x-intercept = 17/5; y-intercept = - 17/3)
- line segment GH : 3x + 5y + 17 = 0 (x-intercept = - 17/3; y-intercept = - 17/5)
- line segment EH : 5x - 3y + 17 = 0 (x-intercept = - 17/5; y-intercept = 17/3)
Slopes of the Line Segments
- mAB = mCD = 1/4
- mAD = mBC = -4
- mEF = mGH = - 3/5
- mFG = mEH = 5/3
Problem 4
.jpg)
Point of Intersection of the Diagonals: E (0, 0)
Distances Between Points
- distanceAB = distanceBC = distanceCD = distanceAD = √ 52
- distanceAC = distanceBD = √ 104
- distanceAE = distanceCE = distanceBE = distanceDE = √ 26
Equations of the Line Segments
- line segment AB : 2x + 3y - 13 = 0 (x-intercept = 13/2; y-intercept = 13/3)
- line segment BC : 3x - 2y - 13 = 0 (x-intercept = 13/3; y-intercept = - 13/2)
- line segment CD : 2x + 3y + 13 = 0 ( x-intercept = - 13/2; y-intercept = - 13/3)
- line segment AD : 3x - 2y + 13 = 0 (x-intercept = - 13/3; y-intercept = 13/2)
- line segment AC : 5x + y = 0 (x-intercept = 0; y-intercept = 0)
- line segment BD : x - 5y = 0 (x-intercept = 0; y-intercept = 0)
Slopes of the Line Segments
- mAB = mCD = - 2/3
- mBC = mAD = 3/2
- mAC = -5
- mBD = 1/5
Problem 5
.jpg)
Point of Intersection of the Diagonals: E (-2, 1)
Distances Between Points
- distanceAB = √ 20
- distanceCD = √ 80
- distanceAD = distanceBC = √ 50
- distanceAC = distanceBD = √ 90
- distanceAE = 1/3 (distanceAC) = (√ 90)/3 = √ 10
- distanceBE = 1/3 (distanceBD) = (√ 90)/3 = √ 10
Equations of the Line Segments
- line segment AB : x - 2y + 9 = 0 (x-intercept = -9; y-intercept = 9/2)
- line segment BC : x + y - 3 = 0 (x-intercept = 3; y-intercept = 3)
- line segment CD : x - 2y - 6 = 0 (x-intercept = 6; y-intercept = -3)
- line segment AD : 7x + y + 33 = 0 (x-intercept = - 33/7; y-intercept = -33)
- line segment AC : x + 3y - 1 = 0 (x-intercept = 1; y-intercept = 1/3)
- line segment BD : 3x - y + 7 = 0 (x-intercept = - 7/3; y-intercept = 7)
Slopes of the Line Segments
- mAB = mCD = 1/2
- mBC = -1
- mAD = -7
- mAC = - 1/3
- mBD = 3
Problem 6
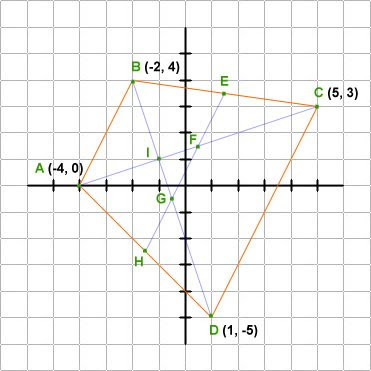.jpg)
Point of Intersection of the Diagonals: I (-1, 1)
Midpoints of
- line segment BC: E (3/2, 7/2)
- line segment AD: H (- 3/2, - 5/2)
- diagonal AC: F (1/2, 3/2)
- diagonal BD: G (- 1/2, - 1/2)
Distances Between Points
- distanceAB = √ 20
- distanceCD = √ 80
- distanceAD = distanceBC = √ 50
- distanceAC = distanceBD = √ 90
- distanceEH = √ 45 = ½( distanceAB + distanceCD ) = ½(√ 20 + √ 80)
- distanceAF = distanceCF = distanceBG = distanceDG = √ 45/2
- distanceAI = 1/3 (distanceAC) = (√ 90)/3 = √ 10
- distanceBI = 1/3 (distanceBD) = (√ 90)/3 = √ 10
Equations of the Line Segments
- line segment AB : 2x - y + 8 = 0 (x-intercept = -4; y-intercept = 8)
- line segment BC : x + 7y - 26 = 0 (x-intercept = 26; y-intercept = 26/7)
- line segment CD : 2x - y - 7 = 0 (x-intercept = 7/2; y-intercept = -7)
- line segment AD : x + y + 4 = 0 (x-intercept = -4; y-intercept = -4)
- line segment AC : x - 3y + 4 = 0 (x-intercept = -4; y-intercept = 4/3)
- line segment BD : 3x + y + 2 = 0 (x-intercept = - 2/3; y-intercept = -2)
- line segment EH : 4x - 2y + 1 = 0 (x-intercept = - 1/4; y-intercept = 1/2)
Slopes of the Line Segments
- mAB = mCD = mEH = 2
- mBC = - 1/7
- mAD = -1
- mAC = 1/3
- mBD = -3
Problem 7

Point of Intersection of the Diagonals: E (1, 0)
Distances Between Points
- distanceAB = distanceBC = distanceCD = distanceAD = √ 40
- distanceAC = √ 128
- distanceBD = √ 32
- distanceAE = distanceCE = √ 32
- distanceBE = distanceDE = √ 8
Equations of the Line Segments
- line segment AB : x + 3y - 9 = 0 (x-intercept = 9; y-intercept = 3)
- line segment BC : 3x + y - 11 = 0 (x-intercept = 11/3; y-intercept = 11)
- line segment CD : x + 3y + 7 = 0 (x-intercept = -7; y-intercept = - 7/3)
- line segment AD : 3x + y + 5 = 0 (x-intercept = - 5/3; y-intercept = -5)
- line segment AC : x + y - 1 = 0 (x-intercept = 1; y-intercept = 1)
- line segment BD : x - y - 1 = 0 (x-intercept = 1; y-intercept = -1)
Slopes of the Line Segments
- mAB = mCD = - 1/3
- mBC = mAD = -3
- mAC = -1
- mBD = 1
Interior Angles of Rhombus ABCD
- angle A = angle C = 53.13°
- angle B = angle D = 126.87°
- angle BAC = angle CAD = angle ACB = angle ACD = 26.57°
- angle ABD = angle CBD = angle BDC = angle ADB = 63.43°