Coordinate Graphs of Quadrilaterals
The illustrated problems given below are graphs of the following quadrilaterals:
- rectangles
- squares
- rhombi
- trapezoids
A quadrilateral is defined as a polygon with four sides.
A parallelogram is a quadrilateral that has two pairs of parallel opposite sides.
Description of Quadrilaterals
Rectangles and rhombi are both parallelograms. However, rhombi have no right interior angles while rectangles have right interior angles.
Generally, a rectangle has one of its two consecutive sides longer than the other one. But a square, which is also a rectangle, has two equal consecutive sides.
Like the square, a rhombus has two equal consecutive sides. But it has no right interior angles.
Lastly, a trapezoid is a quadrilateral with one pair of parallel opposite sides. Its non-parallel sides can be equal or unequal. If a trapezoid has equal non-parallel sides, then it's called an isosceles trapezoid.
Concepts Illustrated By the Problems
Each problem below illustrates the following concepts:- distance between 2 points
- parallel and perpendicular lines
- point of intersection of two straight lines
- equation of a straight line
The equation of a straight line can be determined if any of the following are given:
- 2 points on the line
- slope and a point of the line
- slope and the x-intercept ( or y-intercept ) of the line
- x-intercept and y-intercept of the line
Description of the Problems
For each problem (or graph), the following information are given:- equations of the line segments
- slopes of the line segments
- x-intercepts and y-intercepts of the lines
- distances between the terminal points of the line segments
- points on the extended line segments
Using one or a combination of two or more of the above information, it is possible for a problem to be presented in several ways.
Line segments and their terminal points referred to in the problems are the sides and vertices, respectively, of the quadrilaterals.
Slope of a line segment with terminal points A and B is abbreviated as mAB.
Distance between points A and B is abbreviated as distanceAB
Points on a line refer to the points of the extended line of that line segment.
Graphs of Rectangles
Show that:
- points A(-2, 4), B(-4, 0), C(0, 3), and D(-2, -1) are vertices of a rectangle;
- points A(-2, 4), B(-4, 0), E(4, 1), and F(2, -3) are vertices of a rectangle;
- points C(0, 3), D(-2, -1), E(4, 1), and F(2, -3) are vertices of a square.
.jpg)
Equations of the Line Segments
- line segment AB (2x - y + 8 = 0): x-intercept = -4; y-intercept = 8
- line segment CD (2x - y + 3 = 0): x-intercept = -3/2; y-intercept = 3
- line segment EF (2x - y - 7 = 0): x-intercept = 7/2; y-intercept = -7
- line segment AC or CE or AE (x + 2y - 6 = 0): x-intercept = 6; y-intercept = 3
- line segment BD or DF or BF (x + 2y + 4 = 0): x-intercept = -4; y-intercept = -2
Slopes of the Line Segments
- mAB = mCD = mEF = 2
- mAC = mCE = mAE = - 1/2
- mBD = mDF = mBF = - 1/2
Distances Between Points
- distanceAB = distanceCD = distanceEF = √ 20
- distanceAC = distanceBD = √ 5
- distanceCE = distanceDF = √ 20
- distanceAE = distanceBF = √ 45
Points On The Lines
- line 2x - y + 8 = 0 (line segment AB): (-5, -2), (-4, 0), (-3, 2), (-2, 4), (-1, 6), (1, 10),(2, 12), (3, 14), (4, 16), (5, 18)
- line 2x - y + 3 = 0 (line segment CD): (-5, -7), (-4, -5), (-3, -3), (-2, -1), (-1, 1), (1, 5), (2, 7), (3, 9), (4, 11), (5, 13)
- line 2x - y - 7 = 0 (line segment EF): (-5, -17), (-4, -15), (-3, -13), (-2, -11), (-1, -9), (1, -5), (2, -3), (3, -1), (4, 1), (5, 3)
- line x + 2y - 6 = 0 (line segment AC or CE or AE): (-5, 11/2), (-4, 5), (-3, 9/2), (-2, 4), (-1, 7/2), (1, 5/2), (2, 2), (3, 3/2), (4, 1), (5, 1/2)
- line x + 2y + 4 = 0 (line segment BD or DF or BF): (-5, 1/2), (-4, 0), (-3, -1/2), (-2, -1), (-1, -3/2), (1, -5/2), (2, -3), (3, -7/2), (4, -4), (5, -9/2)
Show that the quadrilateral bounded by the lines 3x - 2y + 8 = 0 and 3x - 2y - 5 = 0 and line segments AB and CD is a rectangle.
.jpg)
Equations of the Line Segments
- line 3x - 2y + 8 = 0: x-intercept = - 8/3; y-intercept = 4
- line 3x - 2y - 5 = 0: x-intercept = 5/3; y-intercept = - 5/2
- line segment AB (2x + 3y - 12 = 0): x-intercept = 6; y-intercept = 4
- line segment CD (2x + 3y + 14 = 0): x-intercept = -7; y-intercept = -14/3
Slopes of the Line Segments
- mAB = mCD = - 2/3
- mAD = mBC = 3/2
Distances Between Points
- distanceAD = distanceBC = √ 52
- distanceAB = distanceCD = √ 13
Points On The Lines
- line 3x - 2y + 8 = 0 (line segment AD): (-5, -7/2), (-4, -2), (-3, -1/2), (-2, 1), (-1, 5/2), (1, 11/2), (2, 7), (3, 17/2), (4, 10), (5, 23/2)
- line 3x - 2y - 5 = 0 (line segment BC): (-5, -10), (-4, -17/2), (-3, -7), (-2, -11/2), (-1, -4), (1, -1), (2, 1/2), (3, 2), (4, 7/2), (5, 5)
- line 2x + 3y - 12 = 0 (line segment AB): (-5, 22/3), (-4, 20/3), (-3, 6), (-2, 16/3), (-1, 14/3), (1, 10/3), (2, 8/3), (3, 2), (4, 4/3), (5, 2/3)
- line 2x + 3y + 14 = 0 (line segment CD): (-5, -4/3), (-4, -2), (-3, -8/3), (-2, -10/3), (-1, -4), (1, -16/3), (2, -6), (3, -20/3), (4, -22/3), (5, -8)
Prove analytically that points A(-5, 2), B(3, 4), C(4, 0) and D(-4, -2) are vertices of a rectangle.
.jpg)
Equations of the Line Segments
- line segment AB : x - 4y + 13 = 0; x-intercept = -13; y-intercept = 13/4
- line segment BC : 4x + y - 16 = 0; x-intercept = 4; y-intercept = 16
- line segment CD : x - 4y - 4 = 0; x-intercept = 4; y-intercept = - 1
- line segment AD : 4x + y + 18 = 0; x-intercept = - 9/2; y-intercept = -18
Slopes of the Line Segments
- mAB = mCD = 1/4
- mAD = mBC = - 4
Distances Between Points
- distanceAB = distanceCD = √ 68
- distanceBC = distanceAD = √ 17
Points On The Lines
- line x - 4y + 13 = 0 (line segment AB): (-5, 2), (-4, 9/4), (-3, 5/2), (-2, 11/4), (-1, 3), (1, 7/2), (2,15/4 ), (3, 4), (4, 17/4), (5, 9/2)
- line 4x + y - 16 = 0 (line segment BC): (-5, 36), (-4, 32), (-3, 28), (-2, 24), (-1, 20), (1, 12), (2, 8), (3, 4), (4, 0), (5, -4)
- line x - 4y - 4 = 0 (line segment CD): (-5, -9/4), (-4, -2), (-3, -7/4), (-2, -3/2), (-1, -5/4), (1, -3/4), (2, -1/2), (3, -1/4), (4, 0), (5, 1/4)
- line 4x + y + 18 = 0 (line segment AD): (-5, 2), (-4, -2), (-3, -6), (-2, -10), (-1, -14), (1, -22), (2, -26), (3, -30), (4, -34), (5, -38)
Graphs of Squares
Show that points A(-1, 3), B(3, 2), C(2, -2) and D(-2, -1) are vertices of a square.
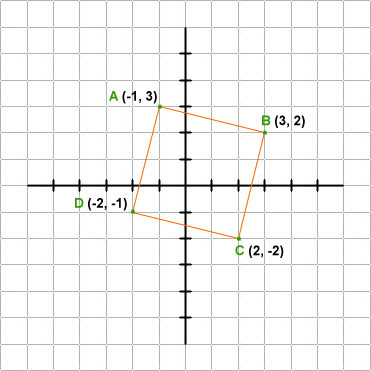.jpg)
Equations of the Line Segments
- line segment AB : x + 4y - 11 = 0; x-intercept = 11; y-intercept = 11/4
- line segment BC : 4x - y - 10 = 0; x-intercept = 5/2; y-intercept = -10
- line segment CD : x + 4y + 6 = 0; x-intercept = -6; y-intercept = -3/2
- line segment AD : 4x - y + 7 = 0; x-intercept = -7/4; y-intercept = 7
Slopes of the Line Segments
- mAB = mCD = - 1/4
- mBC = mAD = 4
Distances Between Points
- distanceAB = distanceBC = distanceCD = distanceAD = √17
Points On The Lines
- line x + 4y - 11 = 0 (line segment AB): (-5, 4), (-4, 15/4), (-3, 7/2), (-2, 13/4), (-1, 3), (1, 5/2), (2, 9/4), (3, 2), (4, 7/4), (5, 3/2)
- line 4x - y - 10 = 0 (line segment BC): (-5, -30), (-4, -26), (-3, -22), (-2, -18), (-1, -14), (1, -6), (2, -2), (3, 2), (4, 6), (5, 10)
- line x + 4y + 6 = 0 (line segment CD): (-5, -1/4), (-4, -1/2), (-3, -3/4), (-2,-1 ), (-1, -5/4), (1, -7/4), (2, -2), (3, -9/4), (4, -5/2), (5, -11/4)
- line 4x - y + 7 = 0 (line segment AD): (-5, -13), (-4, -9), (-3, -5), (-2,-1 ), (-1, 3), (1, 11), (2, 15), (3, 19), (4, 23), (5, 27)
Show that the points of intersection of the following lines are vertices of a square:
- x + y - 4 = 0
- x - y - 4 = 0
- x + y + 4 = 0
- x - y + 4 = 0
.jpg)
Equations of the Line Segments
- line segment AB : x + y - 4 = 0; x-intercept = 4; y-intercept = 4
- line segment BC : x - y - 4 = 0; x-intercept = 4; y-intercept = -4
- line segment CD : x + y + 4 = 0; x-intercept = -4; y-intercept = -4
- line segment AD : x - y + 4 = 0; x-intercept = -4; y-intercept = 4
Slopes of the Line Segments
- mAB = mCD = - 1
- mBC = mAD = 1
Distances Between Points
- distanceAB = distanceBC = distanceCD = distanceAD = √ 32
Points On The Lines
- line x + y - 4 = 0 (line segment AB): (-5, 9), (-4, 8), (-3, 7), (-2, 6), (-1, 5), (1, 3), (2, 2), (3, 1), (4, 0), (5, -1)
- line x - y - 4 = 0 (line segment BC): (-5, -9), (-4, -8), (-3, -7), (-2, -6), (-1, -5), (1, -3), (2, -2), (3, -1), (4, 0), (5, 1)
- line x + y + 4 = 0 (line segment CD): (-5, 1), (-4, 0), (-3, -1), (-2, -2), (-1, -3), (1, -5), (2, -6), (3, -7), (4, -8), (5, -9)
- line x - y + 4 = 0 (line segment AD): (-5, -1), (-4, 0), (-3, 1), (-2, 2), (-1, 3), (1, 5), (2, 6), (3, 7), (4, 8), (5, 9)
Show that the points A(1, 5), B(3, 2), C(0, 0), and D(-2, 3) are vertices of a square.
.jpg)
Equations of the Line Segments
- line segment AB : 3x + 2y - 13 = 0; x-intercept = 13/3; y-intercept = 13/2
- line segment BC : 2x - 3y = 0; x-intercept = 0; y-intercept = 0
- line segment CD : 3x + 2y = 0; x-intercept = 0; y-intercept = 0
- line segment AD : 2x - 3y + 13 = 0; x-intercept = -13/2; y-intercept = 13/3
Slopes of the Line Segments
- mAB = mCD = - 3/2
- mBC = mAD = 2/3
Distances Between Points
- distanceAB = distanceBC = distanceCD = distanceAD = √ 13
Points On The Lines
- line 3x + 2y - 13 = 0 (line segment AB): (-5, 14), (-4, 25/2), (-3, 11), (-2, 19/2), (-1, 8), (1, 5), (2, 7/2), (3, 2), (4, 1/2), (5, -1)
- line 2x - 3y = 0 (line segment BC): (-5, -10/3), (-4, -8/3), (-3, -2), (-2, -4/3), (-1, -2/3), (1, 2/3), (2, 4/3), (3, 2), (4, 8/3), (5, 10/3)
- line 3x + 2y = 0 (line segment CD): (-5, 15/2), (-4, 6), (-3, 9/2), (-2, 3), (-1, 3/2), (1, -3/2), (2, -3), (3, -9/2), (4, -6), (5, -15/2)
- line 2x - 3y + 13 = 0 (line segment AD): (-5, 1), (-4, -5/3), (-3, 7/3), (-2, 3), (-1, 11/3), (1, 5), (2, 17/3), (3, 19/3), (4, 7), (5, 23/3)
Graphs of Rhombi
Prove that points A(1, 5), B(4, 1), C(1, -3) and D(-2, 1) are vertices of a rhombus.
.jpg)
Equations of the Line Segments
- line segment AB : 4x + 3y - 19 = 0; x-intercept = 19/4; y-intercept = 19/3
- line segment BC : 4x - 3y - 13 = 0; x-intercept = 13/4; y-intercept = - 13/3
- line segment CD : 4x + 3y + 5 = 0; x-intercept = - 5/4; y-intercept = - 5/3
- line segment AD : 4x - 3y + 11 = 0; x-intercept = - 11/4; y-intercept = 11/3
Slopes of the Line Segments
- mAB = mCD = - 4/3
- mBC = mAD = 4/3
Distances Between Points
- distanceAB = distanceBC = distanceCD = distanceAD = √ 25
Points On The Lines
- line 4x + 3y - 19 = 0 (line segment AB): (-5, 13), (-4, 35/3), (-3, 31/3), (-2, 9), (-1, 23/3), (1, 5), (2, 11/3), (3, 7/3), (4, 1), (5, -1/3)
- line 4x - 3y - 13 = 0 (line segment BC): (-5, -11), (-4, -29/3), (-3, -25/3), (-2, -7), (-1, -17/3), (1, -3), (2, -5/3), (3, -1/3), (4, 1), (5, 7/3)
- line 4x + 3y + 5 = 0 (line segment CD): (-5, 5), (-4, 11/3), (-3, 7/3), (-2, 1), (-1, -1/3), (1, -3), (2, -13/3), (3, -17/3), (4, -7), (5, -25/3)
- line 4x - 3y + 11 = 0 (line segment AD): (-5, -3), (-4, -5/3), (-3, -1/3), (-2, 1), (-1, 7/3), (1, 5), (2, 19/3), (3, 23/3), (4, 9), (5, 31/3)
Show that points A(-2, 3), B(3, 4), C(2, -1), and D(-3, -2) are vertices of a rhombus.
.jpg)
Equations of the Line Segments
- line segment AB : x - 5y + 17 = 0; x-intercept = -17; y-intercept = 17/5
- line segment BC : 5x - y - 11 = 0; x-intercept = 11/5; y-intercept = -11
- line segment CD : x - 5y - 7 = 0; x-intercept = 7; y-intercept = - 7/5
- line segment AD : 5x - y + 13 = 0; x-intercept = - 13/5; y-intercept = 13
Slopes of the Line Segments
- mAB = mCD = 1/5
- mBC = mAD = 5
Distances Between Points
- distanceAB = distanceBC = distanceCD = distanceAD = √ 26
Points On The Lines
- line x - 5y + 17 = 0 (line segment AB): (-5, 12/5), (-4, 13/5), (-3, 14/5), (-2, 3), (-1, 16/5), (1, 18/5), (2, 19/5), (3, 4), (4, 21/5), (5, 22/5)
- line 5x - y - 11 = 0 (line segment BC): (-5, -36), (-4, -31), (-3, -26), (-2, -21), (-1, -16), (1, -6), (2, -1), (3, 4), (4, 9), (5, 14)
- line x - 5y - 7 = 0 (line segment CD): (-5, -12/5), (-4, -11/5), (-3, -2), (-2, -9/5), (-1, 8/5), (1, -6/5), (2, -1), (3, -4/5), (4, -3/5), (5, -2/5)
- line 5x - y + 13 = 0 (line segment AD): (-5, -12), (-4, -7), (-3, -2), (-2, 3), (-1, 8), (1, 18), (2, 23), (3, 28), (4, 33), (5, 38)
Prove that points A(-5, 2), B(3/5, 4), C(5, 0), and D(-3/5, -2) are vertices of a rhombus.
.jpg)
Equations of the Line Segments
- line segment AB : 5x - 14y + 53 = 0; x-intercept = - 53/5; y-intercept = 53/14
- line segment BC : 10x + 11y - 50 = 0; x-intercept = 5; y-intercept = 50/11
- line segment CD : 5x - 14y - 25 = 0; x-intercept = 5; y-intercept = - 25/14
- line segment AD : 10x + 11y + 28 = 0; x-intercept = - 14/5; y-intercept = - 28/11
Slopes of the Line Segments
- mAB = mCD = 5/14
- mBC = mAD = - 10/11
Distances Between Points
- distanceAB = distanceBC = distanceCD = distanceAD = √ 884/25
Points On The Lines
- line 5x - 14y + 53 = 0 (line segment AB): (-5, 2), (-4, 33/14), (-3, 19/7), (-2, 43/14), (-1, 24/7), (1, 29/7), (2, 9/2), (3, 34/7), (4, 73/14), (5, 39/7)
- line 10x + 11y - 50 = 0 (line segment BC): (-5, 100/11), (-4, 90/11), (-3, 80/11), (-2, 70/11), (-1, 60/11), (0, 50/11), (1, 40/11), (2, 30/11), (3, 20/11), (4, 10/11), (5, 0)
- line 5x - 14y - 25 = 0 (line segment CD): (-5, 25/7), (-4, -45/14), (-3, -20/7), (-2, -5/2), (-1, -15/7), (1, -10/7), (2, -15/14), (3, -5/7), (4, -5/14), (5, 0)
- line 10x + 11y + 28 = 0 (line segment AD): (-5, 2), (-4, 12/11), (-3, 2/11), (-2, -8/11), (-1, -18/11), (1, -38/11), (2, -48/11), (3, -58/11), (4, -68/11), (5, -78/11)
Graphs of Trapezoids
Prove that the points A(-1, 4), B(4, 5), C(-1, -5) and D(-4, -2) are vertices of a trapezoid.
.jpg)
Equations of the Line Segments
- line segment AB : x - 5y + 21 = 0; x-intercept = - 21; y-intercept = 21/5
- line segment BC : 2x - y - 3 = 0; x-intercept = 3/2; y-intercept = - 3
- line segment CD : x + y + 6 = 0; x-intercept = - 6; y-intercept = - 6
- line segment AD : 2x - y + 6 = 0; x-intercept = -3; y-intercept = 6
Slopes of the Line Segments
- mAB = 1/5
- mCD = -1
- mBC = mAD = 2
Distances Between Points
- distanceAB: √ 26
- distanceBC: √ 125
- distanceCD: √ 18
- distanceAD: √ 45
Points On The Lines
- line x - 5y + 21 = 0 (line segment AB): (-5, 16/5), (-4, 17/5), (-3, 18/5), (-2, 19/5), (-1, 4), (1, 22/5), (2, 23/5), (3, 24/5), (4, 5), (5, 26/5)
- line 2x - y - 3 = 0 (line segment BC): (-5, -13), (-4, -11), (-3, -9), (-2, -7), (-1, -5), (1, -1), (2, 1), (3, 3), (4, 5), (5, 7)
- line x + y + 6 = 0 (line segment CD): (-5, -1), (-4, -2), (-3, -3), (-2, -4), (-1, -5), (1, -7), (2, -8), (3, -9), (4, -10), (5, -11)
- line 2x - y + 6 = 0 (line segment AD): (-5, -4), (-4, -2), (-3, 0), (-2, 2), (-1, 4), (1, 8), (2, 10), (3, 12), (4, 14), (5, 16)
Show that points A(- 80/17, 71/17), B(-1, 5), C(2, 0), and D(- 8/17, - 49/17) are vertices of an isosceles trapezoid.
.jpg)
Equations of the Line Segments
- line segment AB : 2x - 9y + 47 = 0; x-intercept = - 47/2; y-intercept = 47/9
- line segment BC : 5x + 3y - 10 = 0; x-intercept = 2; y-intercept = 10/3
- line segment CD : 7x - 6y - 14 = 0; x-intercept = 2; y-intercept = - 7/3
- line segment AD : 5x + 3y + 11 = 0; x-intercept = - 11/5; y-intercept = - 11/3
Slopes of the Line Segments
- mAB = 2/9
- mCD = 7/6
- mBC = mAD = - 5/3
Distances Between Points
- distanceAB = distanceCD = √ 245/17
- distanceBC = √ 34
- distanceAD = √ 1152/17
Points On The Lines
- line 2x - 9y + 47 = 0 (line segment AB): (-5, 37/9), (-4, 13/3), (-3, 41/9), (-2, 43/9), (-1, 5), (1, 49/9), (2, 17/3), (3, 53/9), (4, 55/9), (5, 19/3)
- line 5x + 3y - 10 = 0 (line segment BC): (-5, 35/3), (-4, 10), (-3, 25/3), (-2, 20/3), (-1, 5), (1, 5/3), (2, 0), (3, -5/3), (4, -10/3), (5, -5)
- line 7x - 6y - 14 = 0 (line segment CD): (-5, - 49/6), (-4, -7), (-3, - 35/6), (-2, - 14/3), (-1, - 7/2), (1, - 7/6), (2, 0), (3, 7/6), (4, 7/3), (5, 7/2)
- line 5x + 3y + 11 = 0 (line segment AD): (-5, 14/3), (-4, 3), (-3, 4/3), (-2, -1/3), (-1, -2), (1, -16/3), (2, -7), (3, -26/3), (4, -31/3), (5, -12)
Prove that points A(-4, 1), B(-1, 4), C(5, 1) and D(-1, -5) are vertices of an isosceles trapezoid.
.jpg)
Equations of the Line Segments
- line segment AB : x - y + 5 = 0; x-intercept = - 5; y-intercept = 5
- line segment BC : x + 2y - 7 = 0; x-intercept = 7; y-intercept = 7/2
- line segment CD : x - y - 4 = 0; x-intercept = 4; y-intercept = - 4
- line segment AD : 2x + y + 7 = 0; x-intercept = - 7/2; y-intercept = - 7
Slopes of the Line Segments
- mAB = mCD = 1
- mBC = - 1/2
- mAD = -2
Distances Between Points
- distanceAB = √ 18
- distanceCD = √ 72
- distanceBC = distanceAD = √ 45
Points On The Lines
- line x - y + 5 = 0 (line segment AB): (-5, 0), (-4, 1), (-3, 2), (-2, 3), (-1, 4), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)
- line x + 2y - 7 = 0 (line segment BC): (-5, 6), (-4, 11/2), (-3, 5), (-2, 9/2), (-1, 4), (1, 3), (2, 5/2), (3, 2), (4, 3/2), (5, 1)
- line x - y - 4 = 0 (line segment CD): (-5, -9), (-4, -8), (-3, -7), (-2, -6), (-1, -5), (1, -3), (2, -2), (3, -1), (4, 0), (5, 1)
- line 2x + y + 7 = 0 (line segment AD): (-5, 3), (-4, 1), (-3, -1), (-2, -3), (-1, -5), (1, -9), (2, -11), (3, -13), (4, -15), (5, -17)