Graphs of Inequalities With Two Variables

In the following graphs of inequalities with 2 variables, the color-shaded regions indicate the regions containing the points that satisfy the given inequalities.

For any given inequality with two variables, there is a corresponding equality which is actually an equation of a straight line.

All points lying on the line satisfy the equality; and all points lying outside the line satisfy the corresponding inequalities.

Referring to the illustration below, the line x + 2y = - 2 is given.

All points along the line satisfy the statement x + 2y = - 2; any other points outside of the line will make either of the two corresponding inequality statements true, x + 2y > - 2 or x + 2y < - 2.

The two sets of points (the set of points above the line and the set of points below the line) define two inequalities of opposite directions as indicated in the figure.

The next graph below is for the line x - 3y = - 4 and its corresponding inequalities x - 3y > - 4 and x - 3y < - 4.

Observe that a change in the sign of slope of the line reverses the directions of the inequalities for the sets of points above and below the line.

Based on the above graphs, the following generalizations will be presented here: For any line whose sets of points can be differentiated into sets of points above and below it,

• the set of points above the given line with a negative slope will always satisfy the corresponding inequality with greater than values;
• the set of points below the given line with a positive slope will always satisfy the corresponding inequality with greater than values.

A quick way of determining the slope of a line is to convert its equation into a slope-intercept form, y = mx + b.

The shaded regions of the succeeding four graphs are bounded by dashed lines indicating that the points along the dashed lines do not make the inequality statements true.

Problem 1 Draw the graph of 3x + 2y > 0.



Problem 2 Draw the graph of 3x + 4y < 3.



Problem 3 Construct the graph describing the statement 2x - 5y < -10.



Problem 4 Make a graph of x - y > - 2.

These last four diagrams are about mixed expressions of inequality and equality. The shaded region contains the set of points satisfying the inequality part of the given mixed statement while the solid line border contains the points that satisfy the equality part of the same statement.

Problem 5 Make a graph of x - 4y ≤ 6.



Problem 6 Draw the graph of 3x - 5y ≥ - 3.



Problem 7 Sketch the graph that describes the expression 2x + 3y ≥ 6.



Problem 8 Sketch the graph that describes the expression 3x + 4y ≤ 6.

Graphs of Linear Inequalities

In the following graphs, the shaded part of the number line (in red color) indicates the solution sets of the inequalities.

These problems, 20 in all, illustrate the following axioms (or postulates):

• Axiom 1 A quantity added to both sides of an inequality does not change the direction of inequality.
• Axiom 2 A quantity subtracted from both sides of an inequality does not change the direction of inequality.
• Axiom 3 Multiplying both sides of an inequality by a positive number does not change the direction of inequality.
• Axiom 4 Dividing both sides of an inequality by a positive number does not change the direction of inequality.
• Axiom 5 Multiplying both sides of an inequality by a negative number changes the direction of inequality.
• Axiom 6 Dividing both sides of an inequality by a negative number changes the direction of inequality.

Problems 4, 7, 8, 9, 12, 16 and 19 illustrate axioms 5 and 6.

The rest of the problems illustrate the remaining axioms.

1.	5x + 4 < 3x + 8
	Answer: { x | x < 2 }

2.	x/3 - 3 < -1
	Answer: { x | x < 6 }

3.	2x + 6 > 16
	Answer: { x | x > 5 }

4.	x - 4 ≥ 9x - 60
	Answer: { x | x ≤ 7 }

5.	8x + 5 ≥ 3x + 10
	Answer: { x | x ≥ 1 }

6.	2x - 3 > 9
	Answer: { x | x > 6 }

7.	x - 8 > 6x - 13
	Answer: { x | x < 1 }

8.	4 - 5x > -6
	Answer: { x | x < 2 }

9.	4 - 16x > 8
	Answer: { x | x < - 1/4 }

10.	x/2 + 7 > 9
	Answer: { x | x > 4 }

11.	9x + 5 > 4x + 40
	Answer: { x | x > 7 }

12.	8 - 5x < 5
	Answer: { x | x > 3/5 }

13.	3x/4 + 2 > 8
	Answer: { x | x > 8 }

14.	2x - 5 ≤ x + 1
	Answer: { x | x ≤ 6 }

15.	5x + 3 < 38
	Answer: { x | x < 7 }

16.	7 - 8x < 3
	Answer: { x | x > 1/2 }

17.	4x + 3 ≤ 3x + 10
	Answer: { x | x ≤ 7 }

18.	5x + 7 < -8
	Answer: { x | x < -3 }

19.	2 - 5x < -33
	Answer: { x | x > 7 }

20.	2x - 5 > -21
	Answer: { x | x > -8 }

Coordinate Graphs of Quadrilaterals With Their Diagonals And Medians

The illustrated problems given below are graphs of the following quadrilaterals:

• rectangles
• squares
• rhombus
• trapezoids

Unlike my earlier post about quadrilaterals (see Coordinate Graphs of Quadrilaterals, dated July 2010), these problems focus on the properties of the diagonals and median of quadrilaterals.

These properties are as follows:

• A diagonal divides a parallelogram into two congruent triangles (see Problems 1, 4 and 7).
• Diagonals of a parallelogram bisect each other, that is, the point of intersection of the diagonals is their midpoint (see Problems 1, 4 and 7).
• Midpoints of the sides of a parallelogram, when joined together, form another parallelogram (see Problems 2 and 3).
• Diagonals of a rhombus bisect its angles and are perpendicular to each other (see Problem 7).
• Diagonals of a rectangle are equal (see Problem 1 and 4).
• Diagonals of an isosceles trapezoid are equal (see Problem 5 and 6).
• The point of intersection of the diagonals of an isosceles trapezoid trisects the diagonals (see Problem 5 and 6).
• The median of a trapezoid is parallel to its bases (see Problem 6).
• The median of a trapezoid is equal to one half the sum of its bases (see Problem 6).
• The median of a trapezoid intersects each of its diagonals at their midpoints (see Problem 6).

Concepts Illustrated By the Problems

• distance between two points
• properties of parallel and perpendicular lines
• point of intersection of two straight lines
• equation of a straight line
• midpoint of a line segment
• angle between two lines
• angle bisector

Description of the Problems

Depending on the graph, a combination of the following information are provided:

• equations of the line segments
• slopes of the line segments
• x-intercepts and y-intercepts of the lines
• distances between the terminal points of the line segments
• midpoints of the line segments

Using one or a combination of two or more of the above information, it is possible for a problem to be presented in several ways.

Line segments and their terminal points referred to in the problems are the sides and vertices, respectively, of the quadrilaterals.

Slope of a line segment with terminal points A and B is abbreviated as m_AB.

Distance between points A and B is abbreviated as distance_AB

Problem 1

Point of Intersection of the Diagonals: E (- 1/2, -1)

Distances Between Points

• distance_AB = distance_CD = √ 68
• distance_AD = distance_BC = √ 17
• distance_AC = distance_BD = √ 85
• distance_AE = distance_CE = distance_BE = distance_DE = √ 85/4

Equations of the Line Segments

• line segment AB : x - 4y + 5 = 0 (x-intercept = -5; y-intercept = 5/4)
• line segment BC : 4x + y - 14 = 0 (x-intercept = 14/4; y-intercept = 14)
• line segment CD : x - 4y - 12 = 0 (x-intercept = 12; y-intercept = -3)
• line segment AD : 4x + y + 20 = 0 (x-intercept = -5; y-intercept = -20)
• line segment AC : 2x + 9y + 10 = 0 (x-intercept = -5; y-intercept = -10/9)
• line segment BD : 6x - 7y - 4 = 0 (x-intercept = 2/3; y-intercept = - 4/7)

Slopes of the Line Segments

• m_AB = m_CD = 1/4
• m_AD = m_BC = -4
• m_AC = - 2/9
• m_BD = 6/7

Problem 2

Midpoints of Rectangle ABCD

• E (-1, 9/2)
• F (0, 0)
• G (-3,- 7/2)
• H (-4, 1)

Distances Between Points

• distance_AB = distance_CD = √ 17
• distance_AD = distance_BC = √ 68
• distance_EF = distance_FG = distance_GH = distance_EH = √ 85/4
• distance_AE = distance_BE = distance_CG = distance_DG = √ 17/4
• distance_AH = distance_DH = distance_BF = distance_CF = √ 17

Equations of the Line Segments

• line segment AB : x + 4y - 17 = 0 (x-intercept = 17; y-intercept = 17/4)
• line segment BC : 4x - y = 0 (x-intercept = 0; y-intercept = 0)
• line segment CD : x + 4y + 17 = 0 (x-intercept = -17; y-intercept = - 17/4)
• line segment AD : 4x - y + 17 = 0 (x-intercept = - 17/4; y-intercept = 17)
• line segment EF : 9x + 2y = 0 (x-intercept = 0; y-intercept = 0)
• line segment FG : 7x - 6y = 0 (x-intercept = 0; y-intercept = 0)
• line segment GH : 9x + 2y + 34 = 0 (x-intercept = -34/9; y-intercept = -17)
• line segment EH : 7x - 6y + 34 = 0 (x-intercept = -34/7; y-intercept = 17/3)

Slopes of the Line Segments

• m_AB = m_CD = - 1/4
• m_AD = m_BC = 4
• m_EF = m_GH = - 9/2
• m_EH = m_FG = 7/6

Problem 3

Midpoints of Square ABCD

• E (-1, 4)
• F (4, 1)
• G (1, -4)
• H (-4, -1)

Distances Between Points

• distance_AB = distance_BC = distance_CD = distance_AD = √ 68
• distance_EF = distance_FG = distance_GH = distance_EH = √ 34
• distance_AE = distance_BE = distance_BF = distance_CF = distance_CG = distance_DG = distance_AH = distance_DH = √ 17

Equations of the Line Segments

• line segment AB : x - 4y + 17 = 0 (x-intercept = -17; y-intercept = 17/4)
• line segment BC : 4x + y - 17 = 0 (x-intercept = 17/4; y-intercept = 17)
• line segment CD : x - 4y - 17 = 0 (x-intercept = 17; y-intercept = - 17/4)
• line segment AD : 4x + y + 17 = 0 (x-intercept = - 17/4; y-intercept = -17)
• line segment EF : 3x + 5y - 17 = 0 (x-intercept = 17/3; y-intercept = 17/5)
• line segment FG : 5x - 3y - 17 = 0 (x-intercept = 17/5; y-intercept = - 17/3)
• line segment GH : 3x + 5y + 17 = 0 (x-intercept = - 17/3; y-intercept = - 17/5)
• line segment EH : 5x - 3y + 17 = 0 (x-intercept = - 17/5; y-intercept = 17/3)

Slopes of the Line Segments

• m_AB = m_CD = 1/4
• m_AD = m_BC = -4
• m_EF = m_GH = - 3/5
• m_FG = m_EH = 5/3

Problem 4

Point of Intersection of the Diagonals: E (0, 0)

Distances Between Points

• distance_AB = distance_BC = distance_CD = distance_AD = √ 52
• distance_AC = distance_BD = √ 104
• distance_AE = distance_CE = distance_BE = distance_DE = √ 26

Equations of the Line Segments

• line segment AB : 2x + 3y - 13 = 0 (x-intercept = 13/2; y-intercept = 13/3)
• line segment BC : 3x - 2y - 13 = 0 (x-intercept = 13/3; y-intercept = - 13/2)
• line segment CD : 2x + 3y + 13 = 0 ( x-intercept = - 13/2; y-intercept = - 13/3)
• line segment AD : 3x - 2y + 13 = 0 (x-intercept = - 13/3; y-intercept = 13/2)
• line segment AC : 5x + y = 0 (x-intercept = 0; y-intercept = 0)
• line segment BD : x - 5y = 0 (x-intercept = 0; y-intercept = 0)

Slopes of the Line Segments

• m_AB = m_CD = - 2/3
• m_BC = m_AD = 3/2
• m_AC = -5
• m_BD = 1/5

Problem 5

Point of Intersection of the Diagonals: E (-2, 1)

Distances Between Points

• distance_AB = √ 20
• distance_CD = √ 80
• distance_AD = distance_BC = √ 50
• distance_AC = distance_BD = √ 90
• distance_AE = 1/3 (distance_AC) = (√ 90)/3 = √ 10
• distance_BE = 1/3 (distance_BD) = (√ 90)/3 = √ 10

Equations of the Line Segments

• line segment AB : x - 2y + 9 = 0 (x-intercept = -9; y-intercept = 9/2)
• line segment BC : x + y - 3 = 0 (x-intercept = 3; y-intercept = 3)
• line segment CD : x - 2y - 6 = 0 (x-intercept = 6; y-intercept = -3)
• line segment AD : 7x + y + 33 = 0 (x-intercept = - 33/7; y-intercept = -33)
• line segment AC : x + 3y - 1 = 0 (x-intercept = 1; y-intercept = 1/3)
• line segment BD : 3x - y + 7 = 0 (x-intercept = - 7/3; y-intercept = 7)

Slopes of the Line Segments

• m_AB = m_CD = 1/2
• m_BC = -1
• m_AD = -7
• m_AC = - 1/3
• m_BD = 3

Problem 6

Point of Intersection of the Diagonals: I (-1, 1)

Midpoints of

• line segment BC: E (3/2, 7/2)
• line segment AD: H (- 3/2, - 5/2)
• diagonal AC: F (1/2, 3/2)
• diagonal BD: G (- 1/2, - 1/2)

Distances Between Points

• distance_AB = √ 20
• distance_CD = √ 80
• distance_AD = distance_BC = √ 50
• distance_AC = distance_BD = √ 90
• distance_EH = √ 45 = ½( distance_AB + distance_CD ) = ½(√ 20 + √ 80)
• distance_AF = distance_CF = distance_BG = distance_DG = √ 45/2
• distance_AI = 1/3 (distance_AC) = (√ 90)/3 = √ 10
• distance_BI = 1/3 (distance_BD) = (√ 90)/3 = √ 10

Equations of the Line Segments

• line segment AB : 2x - y + 8 = 0 (x-intercept = -4; y-intercept = 8)
• line segment BC : x + 7y - 26 = 0 (x-intercept = 26; y-intercept = 26/7)
• line segment CD : 2x - y - 7 = 0 (x-intercept = 7/2; y-intercept = -7)
• line segment AD : x + y + 4 = 0 (x-intercept = -4; y-intercept = -4)
• line segment AC : x - 3y + 4 = 0 (x-intercept = -4; y-intercept = 4/3)
• line segment BD : 3x + y + 2 = 0 (x-intercept = - 2/3; y-intercept = -2)
• line segment EH : 4x - 2y + 1 = 0 (x-intercept = - 1/4; y-intercept = 1/2)

Slopes of the Line Segments

• m_AB = m_CD = m_EH = 2
• m_BC = - 1/7
• m_AD = -1
• m_AC = 1/3
• m_BD = -3

Problem 7

Point of Intersection of the Diagonals: E (1, 0)

Distances Between Points

• distance_AB = distance_BC = distance_CD = distance_AD = √ 40
• distance_AC = √ 128
• distance_BD = √ 32
• distance_AE = distance_CE = √ 32
• distance_BE = distance_DE = √ 8

Equations of the Line Segments

• line segment AB : x + 3y - 9 = 0 (x-intercept = 9; y-intercept = 3)
• line segment BC : 3x + y - 11 = 0 (x-intercept = 11/3; y-intercept = 11)
• line segment CD : x + 3y + 7 = 0 (x-intercept = -7; y-intercept = - 7/3)
• line segment AD : 3x + y + 5 = 0 (x-intercept = - 5/3; y-intercept = -5)
• line segment AC : x + y - 1 = 0 (x-intercept = 1; y-intercept = 1)
• line segment BD : x - y - 1 = 0 (x-intercept = 1; y-intercept = -1)

Slopes of the Line Segments

• m_AB = m_CD = - 1/3
• m_BC = m_AD = -3
• m_AC = -1
• m_BD = 1

Interior Angles of Rhombus ABCD

• angle A = angle C = 53.13°
• angle B = angle D = 126.87°
• angle BAC = angle CAD = angle ACB = angle ACD = 26.57°
• angle ABD = angle CBD = angle BDC = angle ADB = 63.43°

Systems of Linear Equations In Three Unknowns

These problems are solved by converting the given system into a system of equations in two unknowns.

I kept the variables to minimum in order to avoid having to compute very large numbers that may distract the students from understanding the methods involved in solving this particular type of algebraic problem.

1.	3x - 5y + 4z = 23 and x - 2y + 2z = 9 and 5x - 6y - 3z = 14
	Answer: x = 7; y = 2; z = 3
2.	5x + 2y - 5z = 0 and 6x + y - 2z = 9 and 5x - 4y - 5z = -30
	Answer: x = 2; y = 5; z = 4
3.	5x - y - z = 14 and 5x - 2y - 3z = 7 and 3x - 2y + 3z = 5
	Answer: x = 4; y = 5; z = 1
4.	4x - 3y + 2z = -1 and 3x + y - 3z = 4 and 6x - y - 4z = -5
	Answer: x = 3; y = 7; z = 4
5.	3x + 6y + z = 11 and 2x - 5y - 5z = -13 and x + 4y + 3z = 11
	Answer: x = 1; y = 1; z = 2
6.	3x + y + 2z = 1 and 3x - y + 6z = -1 and 3x - 2y + 3z = 13
	Answer: x = 4; y = -5; z = -3
7.	5x - 2y - 2z = -8 and x + 6y - z = 0 and 5x + 4y + 2z = 30
	Answer: x = 2; y = 1; z = 8
8.	4x - 3y + z = -14 and 6x + y + 4z = 3 and 2x + 3y + 4z = 17
	Answer: x = -2; y = 3; z = 3
9.	3x - y - z = -9 and 2x + y + z = -1 and x - 5y - 3z = -9
	Answer: x = -2; y = -1; z = 4
10.	2x - y - 3z = -11 and x + 3y + z = 14 and x - 3y - 2z = -13
	Answer: x = 3; y = 2; z = 5
11.	3x + 4y + 4z = 34 and 2x - 3y + 2z = 15 and 2x + y - 3z = 4
	Answer: x = 6; y = 1; z = 3
12.	3x - y + 4z = 6 and x + 3y + z = 15 and 3x - 4y - 3z = -13
	Answer: x = 2; y = 4; z = 1
13.	3x + 3y + 2z = -8 and 3x - 2y - 5z = -8 and 5x + 4y + z = -18
	Answer: x = 1; y = -7; z = 5
14.	x - y + 4z = 4 and 5x + y + 3z = -11 and 5x + 3y + z = -3
	Answer: x = -7; y = 9; z = 5
15.	3x - 2y + 3z = -15 and 5x + 4y + z = -11 and x + 5y + 3z = 16
	Answer: x = -5; y = 3; z = 2
16.	3x + 5y - 2z = 14 and 5x + 3y - 4z = 16 and 3x - 4y + 3z = 20
	Answer: x = 5; y = 1; z = 3
17.	6x + y + 3z = -6 and 7x - 4y + 5z = -2 and x - 6y + 5z = -14
	Answer: x = 3; y = -3; z = -7
18.	6x - y - 6z = 23 and 5x - 4y + z = -20 and x - 6y - 5z = 22
	Answer: x = -2; y = 1; z = -6
19.	5x + 3y - 2z = 15 and 3x + 2y + 3z = 27 and 3x + 5y - 5z = 13
	Answer: x = 1; y = 6; z = 4
20.	4x - 3y + 2z = -2 and 3x - y + 3z = 8 and 6x - y + 4z = 14
	Answer: x = 1; y = 4; z = 3
21.	x - y - 4z = -22 and 5x - y - 3z = 11 and 5x - 3y - z = 3
	Answer: x = 7; y = 9; z = 5
22.	4x - 3y + 2z = 11 and 2x + 3y + z = 10 and 4x + 3y + 4z = 23
	Answer: x = 2; y = 1; z = 3
23.	4x + 3y + 2z = 27 and x + 2y + 3z = 13 and 2x + 3y + z = 18
	Answer: x = 4; y = 3; z = 1
24.	x - 3y - 4z = -33 and x + y - 5z = -38 and x - 5y - z = -8
	Answer: x = 6; y = 1; z = 9
25.	5x - 3y + 5z = -15 and 3x + y + 5z = -1 and 3x - y - 5z = 19
	Answer: x = 3; y = 5; z = -3
26.	x - y - 7z = -8 and 9x - 4y - 5z = 11 and 5x - y + 3z = 18
	Answer: x = 4; y = 5; z = 1
27.	2x - y - 5z = -13 and 2x - 3y - 5z = -17 and x - 2y - 2z = -8
	Answer: x = 2; y = 2; z = 3
28.	x - 3y + 3z = 3 and 2x + y + 2z = 9 and x - y + 2z = 4
	Answer: x = 3; y = 1; z = 1
29.	x - 3y + 6z = 25 and x - 4y + 9z = 38 and x - y + 5z = 24
	Answer: x = 1; y = 2; z = 5
30.	x - 3y + z = -10 and 3x + 3y - 4z = 21 and 2x - y - 3z = -5
	Answer: x = 5; y = 6; z = 3

Coordinate Graphs of Triangles

The illustrated problems below are graphs of the following triangles:

• isosceles triangles
• scalene triangles
• right triangles

Concepts Illustrated By the Problems

• distance between two points
• angle between two lines
• point of intersection of two straight lines
• equation of a straight line

Description of the Problems

For each problem, the following information are given:

• equations of the line segments
• slopes of the line segments
• x-intercepts and y-intercepts of the lines
• distances between the terminal points of the line segments
• interior angles of the triangles

Using one or a combination of two or more of the above information, it is possible for a problem to be presented in several ways.

Line segments and their terminal points referred to in the problems are the sides and vertices, respectively, of the triangles.

Slope of a line segment with terminal points A and B is abbreviated as m_AB.

Distance between points A and B is abbreviated as distance_AB

Graphs of Isosceles Triangles

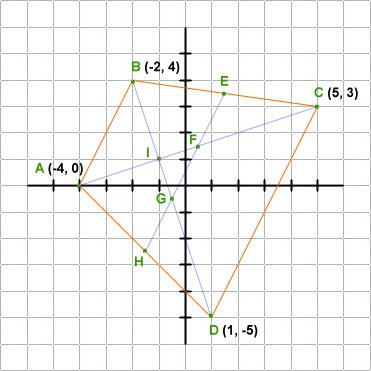
Show that points A(-5, 1), B(3, 5), C(2, -3) are vertices of an isosceles triangle.



Distance Between Two Points

• distance_AB = √ 80
• distance_BC = distance_AC = √ 65

Equations of the Line Segments

• line segment AB: x - 2y + 7 = 0 (x-intercept = -7; y-intercept = 7/2)
• line segment BC: 8x - y - 19 = 0 (x-intercept = 19/8, y-intercept = -19)
• line segment AC: 4x + 7y + 13 = 0 (x-intercept = - 13/4, y-intercept = - 13/7)

Slopes of the Line Segments

• m_AB = 1/2
• m_BC = 8
• m_AC = - 4/7

Interior Angles of the Triangle

• angle A = angle B = 56.3°
• angle C = 67.4°

Show that points A(-5, 4), B(3, 3), C(-1, -4) are vertices of an isosceles triangle.



Distance Between Two Points

• distance_AB = distance_BC = √ 65
• distance_AC = √ 80

Equations of the Line Segments

• line segment AB: x + 8y - 27 = 0 ( x-intercept = 27, y-intercept = 27/8)
• line segment BC: 7x - 4y - 9 = 0 (x-intercept = 9/7, y-intercept = - 9/4)
• line segment AC: 2x + y + 6 = 0 (x-intercept = -3, y-intercept = -6)

Slopes of the Line Segments

• m_AB = - 1/8
• m_BC = 7/4
• m_AC = -2

Interior Angles of the Triangle

• angle A = angle C = 56.3°
• angle B = 67.4°

Prove analytically that points A(-5, -5), B(-2, 6), C(5, -3) are vertices of an isosceles triangle.



Distance Between Two Points

• distance_AB = distance_BC = √ 130
• distance_AC = √ 104

Equations of the Line Segments

• line segment AB: 11x - 3y + 40 = 0 (x-intercept = - 40/11, y-intercept = 40/3)
• line segment BC: 9x + 7y - 24 = 0 (x-intercept = 24/9, y-intercept = 24/7)
• line segment AC: x - 5y - 20 = 0 (x-intercept = 20, y-intercept = -4)

Slopes of the Line Segments

• m_AB = 11/3
• m_BC = - 9/7
• m_AC = 1/5

Interior Angles of the Triangle

• angle A = angle C = 63.4°
• angle B = 53.1°

Graphs of Scalene Triangles

Show that points A(-4, 1), B(1, 0), C(-2, -5) are vertices of a scalene triangle.



Distance Between Two Points

• distance_AB = √ 26
• distance_BC = √ 34
• distance_AC = √ 40

Equations of the Line Segments

• line segment AB: x + 5y - 1 = 0 (x-intercept = 1, y-intercept = 1/5)
• line segment BC: 5x - 3y - 5 = 0 (x-intercept = 1, y-intercept = - 5/3)
• line segment AC: 3x + y + 11 = 0 (x-intercept = - 11/3, y-intercept = -11)

Slopes of the Line Segments

• m_AB = - 1/5
• m_BC = 5/3
• m_AC = -3

Interior Angles of the Triangle

• angle A = 60.3°
• angle B = 70.3°
• angle C = 49.4°

Show that the following points are vertices of a scalene triangle:

• A (-5, -4)
• B (3, 4)
• C (4, -2)

Distance Between Two Points

• distance_AB = √ 128
• distance_BC = √ 37
• distance_AC = √ 85

Equations of the Line Segments

• line segment AB: x - y + 1 = 0 (x-intercept = -1, y-intercept = 1)
• line segment BC: 6x + y - 22 = 0 (x-intercept = 11/3, y-intercept = 22)
• line segment AC: 2x - 9y - 26 = 0 (x-intercept = 13, y-intercept = - 26/9)

Slopes of the Line Segments

• m_AB = 1
• m_BC = -6
• m_AC = 2/9

Interior Angles of the Triangle

• angle A = 32.5°
• angle B = 54.5°
• angle C = 93.0°

Show that the points A(-3, 5), B(5, -2), C(-1, -5) are vertices of a scalene triangle.



Distance Between Two Points

• distance_AB = √ 113
• distance_BC = √ 45
• distance_AC = √ 104

Equations of the Line Segments

• line segment AB: 7x + 8y - 19 = 0 (x-intercept = 19/7, y-intercept = 19/8)
• line segment BC: x - 2y - 9 = 0 (x-intercept = 9, y-intercept = - 9/2)
• line segment AC: 5x + y + 10 = 0 (x-intercept = -2, y-intercept = -10)

Slopes of the Line Segments

• m_AB = - 7/8
• m_BC = 1/2
• m_AC = -5

Interior Angles of the Triangle

• angle A = 37.5°
• angle B = 67.8°
• angle C = 74.7°

Graphs of Right Triangles

Prove that points A(-1, 5), B(5, -1), C(-4, 2) are vertices of a right triangle.

Distance Between Two Points

• distance_AB = √ 72
• distance_BC = √ 90
• distance_AC = √ 18

Equations of the Line Segments

• line segment AB: x + y - 4 = 0 (x-intercept = 4, y-intercept = 4)
• line segment BC: x + 3y - 2 = 0 (x-intercept = 2, y-intercept = 2/3)
• line segment AC: x - y + 6 = 0 (x-intercept = -6, y-intercept = 6)

Slopes of the Line Segments

• m_AB = -1
• m_BC = - 1/3
• m_AC = 1

Interior Angles of the Triangle

• angle A = 90.0°
• angle B = 26.6°
• angle C = 63.4°

Show that points A(-5, 3), B(2, -1), C(-1, -3) are vertices of a right triangle.



Distance Between Two Points

• distance_AB = √ 65
• distance_BC = √ 13
• distance_AC = √ 52

Equations of the Line Segments

• line segment AB: 4x + 7y - 1 = 0 (x-intercept = 1/4, y-intercept = 1/7)
• line segment BC: 2x - 3y - 7 = 0 (x-intercept = 7/2, y-intercept = - 7/3)
• line segment AC: 3x + 2y + 9 = 0 (x-intercept = -3, y-intercept = - 9/2)

Slopes of the Line Segments

• m_AB = - 4/7
• m_BC = 2/3
• m_AC = - 3/2

Interior Angles of the Triangle

• angle A = 26.6°
• angle B = 63.4°
• angle C = 90.0°

Prove that points A(-2, 5), B(4, -3), C(0, -6) are vertices of a right triangle.



Distance Between Two Points

• distance_AB = √ 100
• distance_BC = √ 25
• distance_AC = √ 125

Equations of the Line Segments

• line segment AB: 4x + 3y - 7 = 0 (x-intercept = 7/4, y-intercept = 7/3)
• line segment BC: 3x - 4y - 24 = 0 (x-intercept = 8, y-intercept = -6)
• line segment AC: 11x + 2y + 12 = 0 (x-intercept = - 12/11, y-intercept = -6)

Slopes of the Line Segments

• m_AB = - 4/3
• m_BC = 3/4
• m_AC = - 11/2

Interior Angles of the Triangle

• angle A = 26.6°
• angle B = 90.0°
• angle C = 63.4°

Graphs of Isosceles Right Triangles

Prove that the points A(-4, 1), B(1, 5), C(0, -4) are vertices of an isosceles right triangle.



Distance Between Two Points

• distance_AB = √ 41
• distance_BC = √ 82
• distance_AC = √ 41

Equations of the Line Segments

• line segment AB: 4x - 5y + 21 = 0 (x-intercept = - 21/4, y-intercept = 21/5)
• line segment BC: 9x - y - 4 = 0 (x-intercept = 4/9, y-intercept = -4)
• line segment AC: 5x + 4y + 16 = 0 (x-intercept = - 16/5, y-intercept = -4)

Slopes of the Line Segments

• m_AB = 4/5
• m_BC = 9
• m_AC = - 5/4

Interior Angles of the Triangle

• angle A = 90°
• angle B = 45°
• angle C = 45°

Show that points A(-5, 4), B(0, 2), C(-2, -3) are vertices of an isosceles right triangle.



Distance Between Two Points

• distance_AB = √ 29
• distance_BC = √ 29
• distance_AC = √ 58

Equations of the Line Segments

• line segment AB: 2x + 5y - 10 = 0 (x-intercept = 5, y-intercept = 2)
• line segment BC: 5x - 2y + 4 = 0 (x-intercept = - 4/5, y-intercept = 2)
• line segment AC: 7x + 3y + 23 = 0 (x-intercept = - 23/7, y-intercept = - 23/3)

Slopes of the Line Segments

• m_AB = - 2/5
• m_BC = 5/2
• m_AC = - 7/3

Interior Angles of the Triangle

• angle A = 45°
• angle B = 90°
• angle C = 45°

Prove that points A(-3, 4), B(5, 1), C(-6, -4) are vertices of an isosceles right triangle.



Distance Between Two Points

• distance_AB = √ 73
• distance_BC = √ 146
• distance_AC = √ 73

Equations of the Line Segments

• line segment AB: 3x + 8y - 23 = 0 (x-intercept = 23/3, y-intercept = 23/8)
• line segment BC: 5x - 11y - 14 = 0 (x-intercept = 14/5, y-intercept = - 14/11)
• line segment AC: 8x - 3y + 36 = 0 (x-intercept = - 9/2, y-intercept = 12)

Slopes of the Line Segments

• m_AB = - 3/8
• m_BC = 5/11
• m_AC = 8/3

Interior Angles of the Triangle

• angle A = 90°
• angle B = 45°
• angle C = 45°